As you may have read in some previous post I am actually working on a modified version of the Grover‘s Algorithm. For those who don’t know the principles of Grover’s Algorithm, here is a quick explanation.
We have a function $$f : \mathbb{Z}_2^n\rightarrow \mathbb{Z}_2$$ that is True for only one $$a \in \mathbb{Z}_2^n$$. We also have a quantum oracle that returns the value of the function f. Classicaly, finding the value of $$a$$ will take n-1 steps. With the quantum version (Grover’s Algorithm) it takes only $$\sqrt{n}$$ steps.
The idea (without explanations) is to take an equally distributed weights vector as input $$x$$, and to iterate a sequence of unitary operations during a certain amount of time. After this given number of steps a measurement on the input vector is made, and is has been proved that we will observed the correct answer with probability 1. The number of steps is proportional to $$\sqrt{n}$$.
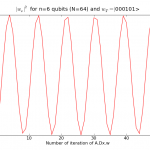
Bellow I put the picture representing the evolution (step after step) of the probability to observe the correct answer. You can see the oscillations that are well explained by geometrical description of this algorithm.
Python Code
Bellow you’ll find the code associated to this example. You’ll also be able to visualize the animation of the probabilities distribution according to the time. The code is written in Python and requires Numpy to work. The associated functions classes are not useful for this simple case, but you’ll understand in the coming post why I need them.
- Grover Algorithm – Python (run python grover.py)[
As you may have read in some previous post I am actually working on a modified version of the Grover‘s Algorithm. For those who don’t know the principles of Grover’s Algorithm, here is a quick explanation.
We have a function $$f : \mathbb{Z}_2^n\rightarrow \mathbb{Z}_2$$ that is True for only one $$a \in \mathbb{Z}_2^n$$. We also have a quantum oracle that returns the value of the function f. Classicaly, finding the value of $$a$$ will take n-1 steps. With the quantum version (Grover’s Algorithm) it takes only $$\sqrt{n}$$ steps.
The idea (without explanations) is to take an equally distributed weights vector as input $$x$$, and to iterate a sequence of unitary operations during a certain amount of time. After this given number of steps a measurement on the input vector is made, and is has been proved that we will observed the correct answer with probability 1. The number of steps is proportional to $$\sqrt{n}$$.
Bellow I put the picture representing the evolution (step after step) of the probability to observe the correct answer. You can see the oscillations that are well explained by geometrical description of this algorithm.
Python Code
Bellow you’ll find the code associated to this example. You’ll also be able to visualize the animation of the probabilities distribution according to the time. The code is written in Python and requires Numpy to work. The associated functions classes are not useful for this simple case, but you’ll understand in the coming post why I need them.
- Grover Algorithm – Python (run python grover.py)
Interesting fact:
If you use more than one correct possible answer (as in the case of perceptron learning) and a different matrix (namely with two -1 instead of only one), the behaviour could be close to the Grover’s Algorithm. Since I was studying perceptron, I implemented a function that output an oracle given a certain threshold. If this threshold is 0, then only one correct answer exist. If it’s one, then n+1 correct answers are possible … but they are all in relation with the initial teacher.
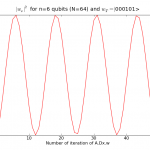
If we fix the teacher, select a threshold of 1, and use the matrix H.diag(-1,1,…,1,-1).H and apply the same algorithm we get the following probability distribution for the teacher :
If you want to use my code, you have to put teachers=mat_teacher_bin(N,1) on line 36 and uncomment line 69
Explainations? For the moment none. But I plan to read the following paper : Improved bond in Oracle identification